Interpolations linéaires de BCRP

Une image au format full-HD (1920x1080 pixels) est constituée de plus de deux millions de pixels. Puis chaque pixel étant décomposé en trois couleurs (rouge, vert, bleu), il faut 6 millions de valeurs pour enregistrer l'image numériquement. En comparaison, il faut seulement 156 valeurs numériques pour mémoriser la composition d'une image avec Spline screen, quelque soit le format de l'image et dans certains cas avec un peu de texte curviligne en plus. À partir de ce concept, on peut surtout dessiner de la géométrie, des abstractions et c'est suffisant pour s'amuser un peu.

La géométrie est artistique

L'histoire de l'art témoigne des artistes qui se sont penchés sur l'abstraction. Le simple plaisir d'agencer des couleurs ensemble est un point de départ. Le programme Spline screen permet de jouer avec les couleurs et les formes. Pour corser le jeu, on peut tenter de représenter quelque chose de déjà existant, comme une peinture célèbre d'un maître de l'abstraction. C'est ce que j'appelle BCRP : des Courbes de Bézier Refont de la Peinture. Petit à petit, une collection de BCRP voit le jour et ouvre un nouveau champ d'investigation : la découverte de l'espace séparant les images.

Interpolation numérique

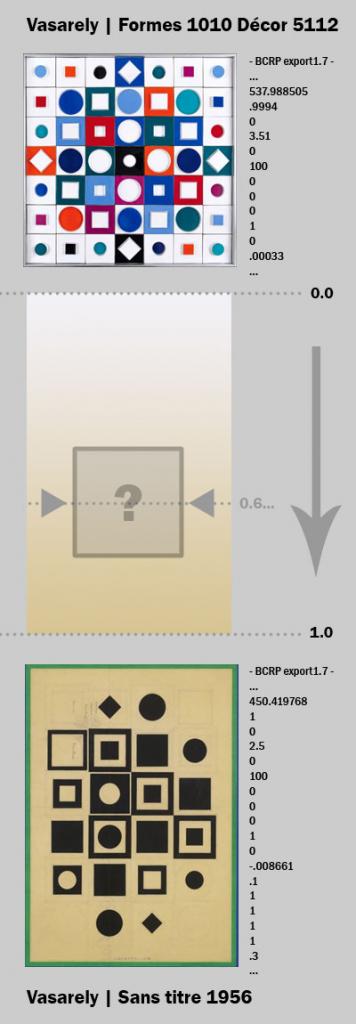
Que se passe-t-il entre 0 et 100 ? À mi-parcours nous pouvons assurément rencontrer 50 ! Reconstituer des valeurs intermédiaires est une technique mathématique https://fr.wikipedia.org/wiki/Interpolation_... qui reste simple dans le cas des variations linéaires. Considérons maintenant deux ensembles, je dirais même deux vecteurs de 156 valeurs numériques (2 images BCRP), il existe alors une multitude de données intermédiaires (vecteurs) correspondant à tel ou tel mi-parcours entre ces deux positions. Parfois, le hasard fait qu'à une position bien choisie, le vecteur calculé produit une image intéressante dans Spline screen ! Voici un exemple dans cet article. Le point de départ étant un premier essai de BCRP avec une composition de Vasarely. Le point d'arrivée est une autre œuvre du peintre, suffisamment simple, en noir sur papier, sans-titre 1956. La troisième image obtenue (à voir en fin d'article) se situe à 48% du départ, équivalent à 52% de l'arrivée. C'est presque à mi-parcours, on y retrouve bien un air de famille entre la première et la deuxième.