Collisions dans un espace fini sans bords

Une histoire d'embouiteillage dans un papier peint

Nouveauté

Imaginons qu'on regarde de près une scène de papier peint avec un décor de voitures. Si deux voitures sont en situation de se percuter et si on se déplace pour regarder un peu plus loin dans le décor, on va retrouver à un moment le même carambolage. Ce petit univers n'est pas infini car on a vite fait le tour des éléments du décor. Pourtant il n'a pas vraiment de bord car on peut se déplacer aussi loin qu'on veut pour regarder le décor, à droite à gauche, en haut en bas. Ce n'est que le mur où est posé le papier peint qui en fixe la limite.

La surface d'une sphère, comme la Terre, est un bon exemple d'espace fini sans bord. Déterminer la collision entre deux objets à la surface de la Terre n'est pas très difficile à imaginer. Mais ça se complique un peu quand on veut faire ce même calcul sur la surface d'un papier peint ! Dans le schéma ci-dessous, j'aborde le raisonnement pour le calcul de la distance entre deux objets. Pour simplifier, il ne s'agit pas de voitures, mais de disques.

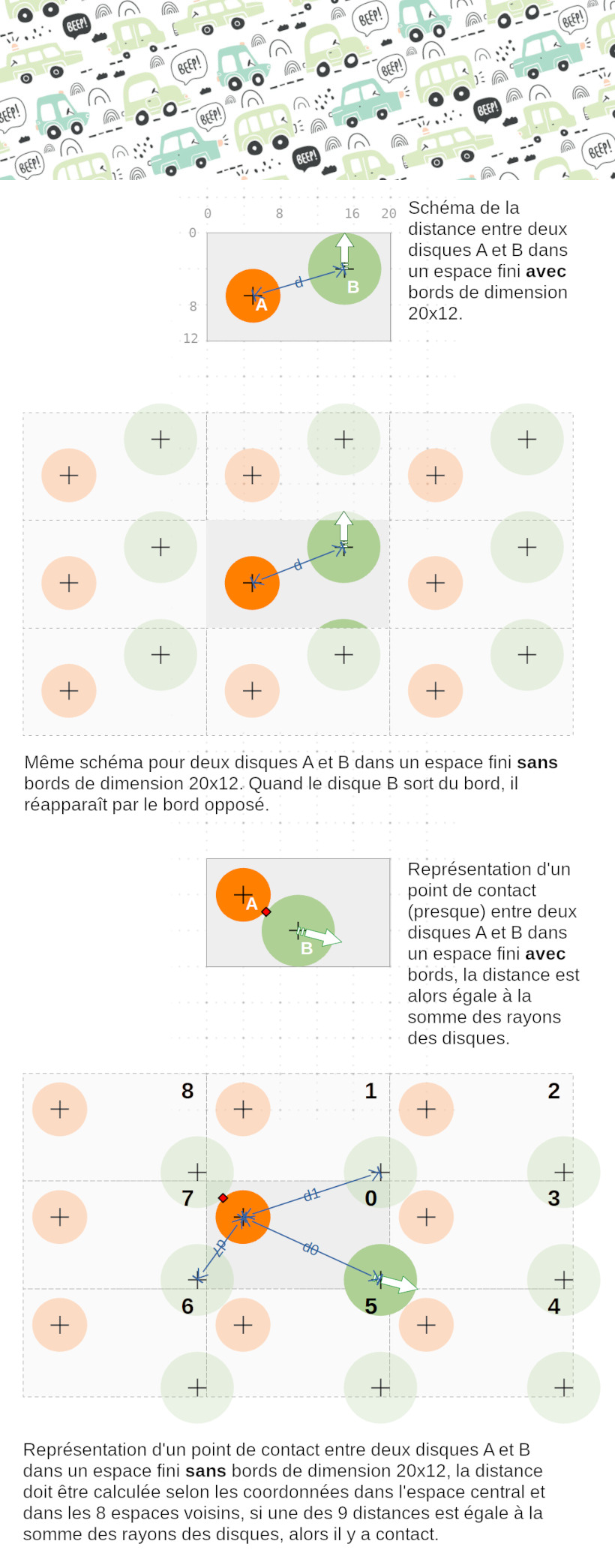
Image article, Quatre schémas pour illustrer les situations dans un espace rectangulaire, avec ou sans bords — Quatre schémas pour illustrer les situations dans un espace rectangulaire, avec ou sans bords

fin

Quelques explictions en plus avec une mise en pratique des calculs

Premier schéma, distance entre les centres des disques : le disque orange A de rayon 3 est positionné en coordonnées x y (5, 7) et le disque vert B de rayon 4 en (15, 4). La distance est alors :

d = sqrt( (5 - 15)^2 + (7 - 4)^2 ) = 10,4

Troisième schéma, contact simple dans le plan : le disque A est positionné en (4, 4) et le disque B en (10, 8). La distance est alors :

d = sqrt( (4 - 10)^2 + (4 - 8)^2 ) = 7,2 très proche de 3 + 4 = 7. 7 est la somme des rayons des deux disques. Les deux disques sont presque en contact.

Quatrième schéma, contact dans le plan fini sans bords : le disque A est positionné toujours en (4, 4) et le disque B est maintenant en (19, 11). La distance dans l'espace central n°0 est :

d0 = sqrt( (4 - 19)^2 + (4 - 11)^2 ) = 16,6 ce qui est très supérieur à 7, il n'y a pas contact.

Mais lorsqu'on calcul la distance avec le disque vert dans l'espace équivalent n°8 (voisin en haut à gauche), le disque est déplacé par translation de vecteur ( - largeur de l'espace, - hauteur de l'espace) :

d8 = sqrt( (4 - (19 - 20))^2 + (4 - (11 - 12))^2 ) = sqrt( 5^2 + 5^2 ) = 7,07 encore plus proche de 7, là les deux disques sont presqu'en contact.

Illustration de papier peint voitures par Sampaj : https://wallpapers.com/wallpapers/car-patter...

En lien

Avec Escher
> Donald Coxeter, pionnier du voyage non-euclidien
> Escher